NLPを使った動線計算

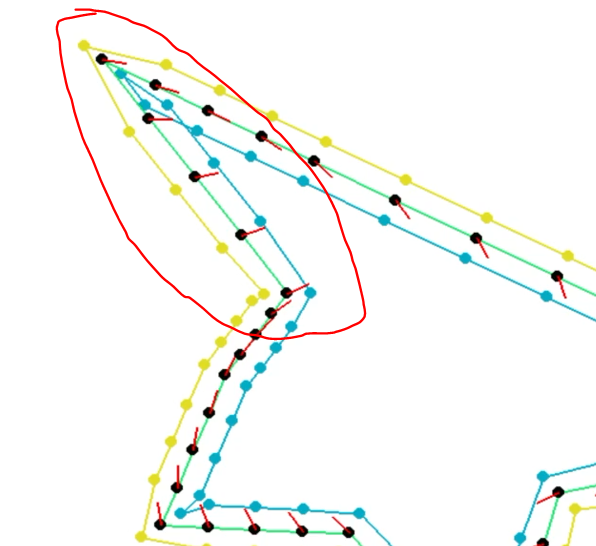
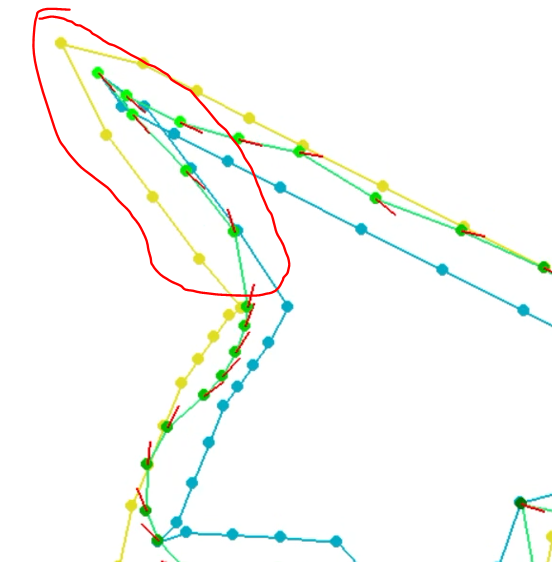
パスプランニングとは、レースカーが与えられたコースを通るための最適なパスを計算する課題である。 以下の例では、最適な経路（レーシングライン）の各点における車の位置、速度、向きを解きます。

RRT*に基づくパスプランニングのアプローチを開発した後、私の友人であるReid Dyeが、この問題を解くためのノンリニアプログラミングに基づく方法を紹介してくれました。彼の方法は、より速く、より正確で、摩擦や速度の制約など、よりカスタマイズ可能で、全体的に整理されていた。 そこで私は、彼のやり方を真似て、NLP（非線形計画法）ベースのソリューションを作ることにした。 以下はその要約である。

最終解 Link to heading

いくつかの点で経路を解いた後、細分化アルゴリズムが経路を0.1秒単位に分割し、最終経路に多くのデータ点を持つようにします。 軌跡に急な角度がある場合、方位の初期推測は本来あるべき方向とは逆の方向を向いている可能性があり、これは通常ソルバーを混乱させ、実行不可能な解に収束させます。これは、より賢い初期推測を使えば解決可能ですが、楽しい問題ではないので、解決しないことにしました。

DeepL.com（無料版）で翻訳しました。

その仕組み Link to heading

ReidはFEBチーム全体のために、アプローチの説明を作ってくれました。 私の実装では、固定された最大速度と最大加速度で一定のホイールトルクを想定しています。 また、一定の加速エンベロープを想定しています。

プロセス Link to heading

私が直面した問題は以下の通りです：

• 私は車両のダイナミクスを（sinhとcoshを使って）明示的に解いたので、ステアリングが0に設定されているとき、車両のダイナミクスは0による除算を持っていました。

def continuous_dynamics_fixed_x_order(x, u, car_params={'l_r': 1.4987, 'l_f':1.5213, 'm': 1.}):
        """Defines dynamics of the car, i.e. equality constraints.
        parameters:
        state x = [xPos,yPos,v,theta]
        input u = [F,phi]
        """
        beta = arctan(car_params['l_r']/(car_params['l_f'] + car_params['l_r']) * tan(u[1]))
        xdot = x[2]*cos(x[3] + beta)
        ydot = x[2]*sin(x[3] + beta)
        vdot = u[0]
        thetadot = x[2] / car_params['l_r'] * sin(beta)

        return vertcat(xdot,
                        ydot,
                        vdot,  
                        thetadot)                 
    
    def discrete_custom_integrator(n = 3, car_params={'l_r': 1.4987, 'l_f':1.5213, 'm': 1.}):
        x0 = MX.sym('x0', 4)
        u = MX.sym('u', 2)
        dt = MX.sym('t')
        xdot = NLPSolver.continuous_dynamics_fixed_x_order(x0, u, car_params)
        f = Function('f', [x0, u], [xdot])
        
        x = x0
        for i in range(n):
            xm = x + f(x, u)*(dt/(2*n))
            x = x+f(xm, u)*(dt/n)
        return Function('integrator', [x0, u, dt], [x])

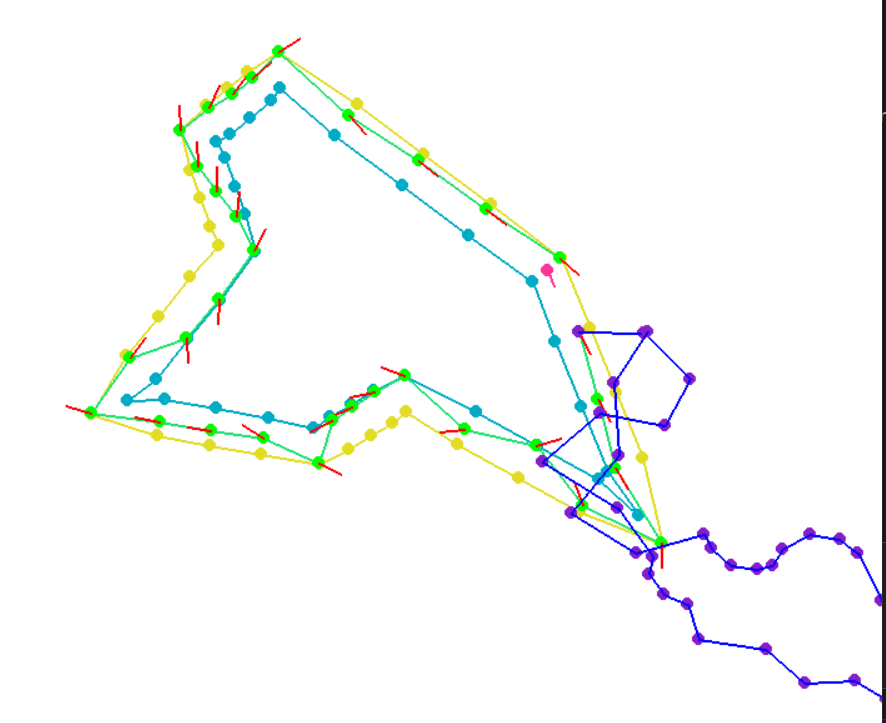
• ソルバーは実現不可能なローカルポイントに収束し続け、ソルバーが示すパスは車のダイナミクスを完全に無視していた。どの点を計算しようとしているかに関係なく、ダイナミクス計算のたびに最初のコントロール入力を渡していたことがわかった（u[i, :]とu[:, i]を間違えていた）。下の紫色のパスは、車のダイナミクスと制御入力に基づいて生成されたパスです（出力されたパスとは異なっているのがわかります）。この問題は単純なのだが、理解するのに時間がかかりすぎた。私は自分のダイナミクスをテストするために、矢印キーを使ってダイナミクスに従って車をコントロールできるようにゲームも作りました。

• 最初の推測はかなり良い推測でなければなりません。最初の推測を行う最も簡単な方法は、中点をたどり、ヘディングを0から2piまで回転するように設定することです。しかし、軌道に急な角度がある場合、ヘディングの初期推測は本来あるべき方向とは逆の方向を向いている可能性があり、これは通常ソルバーを混乱させ、実行不可能な解に収束させてしまいます。