I implimented bezier curves for Berkeley’s formula electric team. I found many websites covered the math side, but was not very clear on how to impliment it, so I will summerize how I implimented it.

To jump to the practical implimentation in python, scroll down to the Practical implimentation section.

Click here for the parent post about Formula Electric in general

The problem: Link to heading

We are given a set of points, and want to construct a curve that smoothly goes though all of these points. This is slightly different than the usual bezier curve problem of having 2 points to go through and two “control” points that dictate the shape of the curve in between.

1 segment bezier curve (with basis math) Link to heading

We atsrat off with the traditionl problem of having 2 points to go through and two “control” points that dictate the shape of the curve in between.

geometric construction Link to heading

One way to construct a bezier curve is as follows:

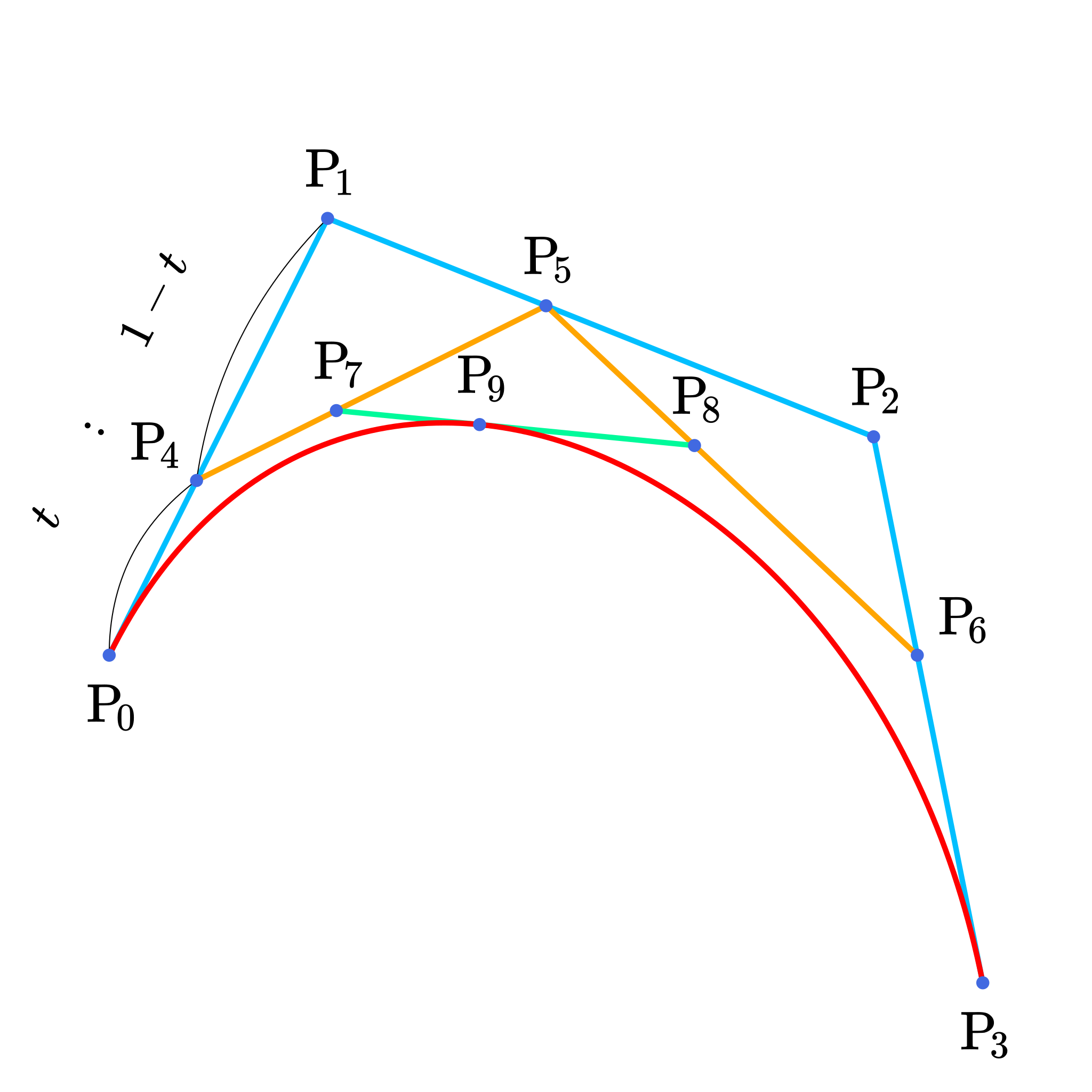
Set a ratio T between 0 and 1. T will serve as what part of the bezier curve we are constructing. For example, setting T = 0.5 means we are constructing the half way point on the curve (and will be taking midpoints).

Setting T = 0.2 means we will be calcuating the point 20% along the bezier curve path.

You can imagine a program would calculate points by setting T = 1%, 2%, … 99% to get a approximate curve.

Take the three line segments connecting your original three points (P0, P1, P2, P3) and make three more points T along each line segment (P4, P5, P6). So if T = 0.5, then we take midpoints.

Then connect (P4, P5) and (P5, P6). Repeat a similar process of creating two more points T along the line segments (P4, P5) and (P5, P6).

Connecting those two and taking the point T along that line will result in the Point on the Bezier curve.

The image above should make these instructions clear.

construction by basis Link to heading

Although the previous method is geometric, it is a bit convoluted to program. We would like to have analytical solutions instead of having to draw lines and take points along those lines. Here is where a bit of linear algebra comes in.

It turns out we can define the bezier curve another way that makes it easier to decompose analytically.

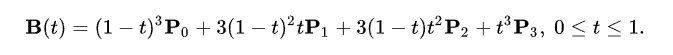
Notice the coefficints in front of each point: t^3, 3t^2(1-t), 3t(1-t)^2, (1-t)^3

The bezier curve is defined as a weighted sum of the four points (2 start/end points and 2 control points). depending on what the value of the coefficiants in front of each point is, the weights of the four points change.

An interesting property of these coefficiants is:

The coefficients sum to 1 for ANY t. (Even when giving uneven weights to certain elements, you expect that total probability(or sum of weights) to be 1)

The sum of the curves at any t is 1, but the relative weights (importance) of each curve is changing.

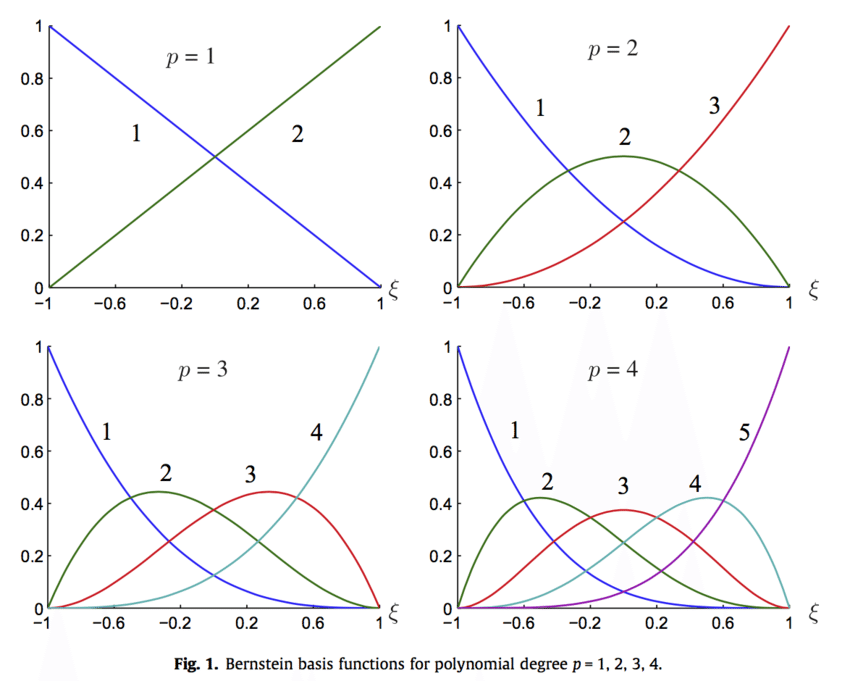
This should make sense, because if for example you wanted to divide a cake between friends, but some friends are more hungry then others, you might suggest a weighted division where people get slices proportional to how hungry they are. But no matter how the portions (weights) end up, the sum of these weights needs to be 1 because no cake can be destroyed or created out of nowhere.

For those with liner algebra background, you can think of these polynomials as a basis for the solution space of bezier curves with the points being the representation of the curve in this basis.

So with this definition, you dont need to construct lines and take points along them anymore: You just need to plug in your 4 points in to the equation and plug in the T value you desire to get the point on the bezier curve.

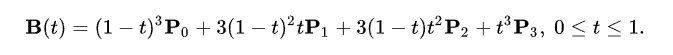
But we still have a problem… We dont get “control” points. All we have are points we need to go through. this leads us to the next section specific to our path finding problem:

Constraints Link to heading

Our main issue now is that we dont have control points (points P1 and P2). But by framing our constraints a different, way, we can calcuate what these control points should be for each segment based on just the coordinates of the points we wnt to go through.

So instead of having our conditions in terms of control points which are hard to take advantage of, we will translate them into statements that we can use to generate a system of equations that give us the coordinates of where the control points should be in terms of the points we want to pass through.

• Our solution must pass through the given points (same conditions as the situation with control points)
• The derivitive at the end of one segment needs to be the same as the derivitive at the start of the next segment. This is needed to avoid any sharp corners, and is a very important condition (possibly the core property we want to have bezier curves for).
• The second derivitive at the the of one segment needs to be the same as the second derivitive of the next segment. This provides a smoother overall curve

But we are missing two conditions at either end because we dont have constraints on the derivitive or second derivitive on the ends. So an additional constraint is

• The derivitive at the ends needs to be 0 i.e the curve should be linear at the ends.

We have now converted constraints we didnt have (the two control points per segment) to constraints we can take advantage of: the derivitive at the endpoints of segment.

we should end up with 2n - 2 equations for 2n unknowns (2 control points per segment), and combined with 2 equations from the derivitives being 0 at the ends will yield a unique solution.

My implimentation is heavily based on this article BE WARE THERE IS A TYPO IN THE ABOVE WEBSITE: P2(i) = 2K(i) - P1(i) should be P2(i) = 2K(i+1) – P1(i+1)